Observation Vs Ground Truth And Why Data Analysts Are Important
Relationship between Observation and Ground truth
While reviewing probability and statistics for my Regression Analysis class, I worked on a probability problem:
3 prisoners are informed by their jailer that one of them has been chosen at random to be executed, and the other 2 are to be freed. Prisoner A asks the jailer to tell him privately which of his fellow prisoners will be set free, claiming that there would be no harm in divulging this information, since he already knows that at least one will go free. The jailer refuses by arguing that if A knew, A’s probability of being executed would rise from 1/3 to 1/2 (i.e., there would only be 2 prisoners left). Whose reasoning is correct and why? [1]
The main purpose of the problem is to practice conditional probability using Bayes Theorem. At first, I thought the problem was not that difficult and provide a answer as follow:

I was convinced that the Jailer’s reasoning was correct, that knowing the name of one of his cell-mate who will go free would help prisoner A reasons his chance to 1/2. Only when I looked at the solution, I realized that I was wrong.
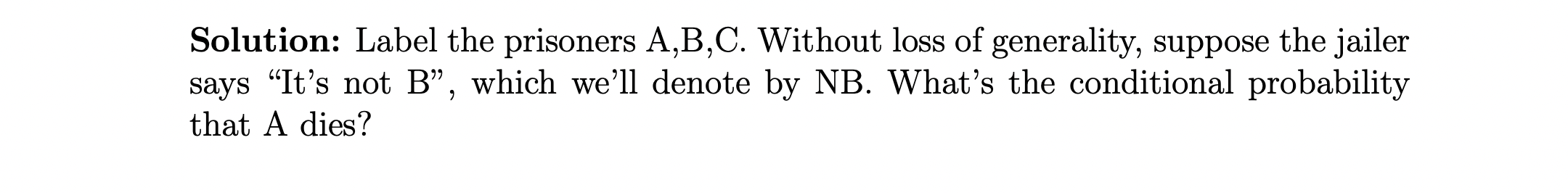
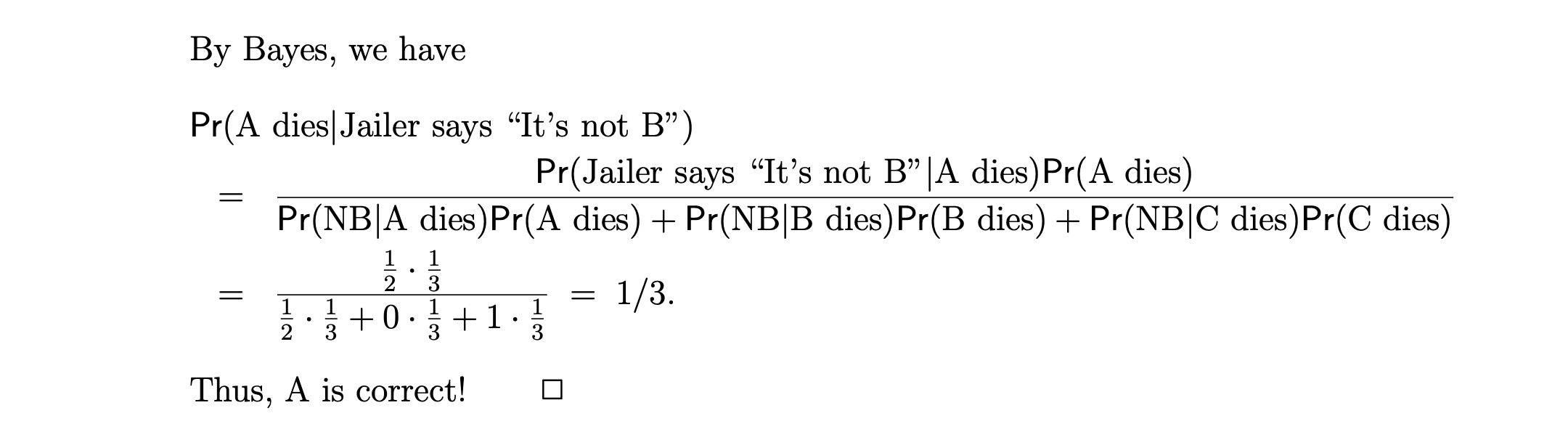
My initial answer didn’t realize the difference between Observation (Jailer saying “Not B” - $NB$) and Ground truth (B go free - $\bar{B}$). In this case, the Observation $NB$ is also a random variable created from the Jailer’s process to answer prisoner A’s questions:
- If A was to be executed, then the Jailer would choose randomly B or C to tell A one name of the other prisoner who would go free. Thus $Pr(NB) = Pr(NC) = 0.5$
- If B was to be executed, then the Jailer must tell A that C will go free. Thus $Pr(NB) = 0$
- If C was to be executed, then the Jailer must tell A that B will go free. Thus $Pr(NB) = 1$
We can clearly see that this process create a probabilistic mapping between the Ground truth and the Observation:
| Ground truth | Observation |
|---|---|
| $A$ | $NB$ (50%) or $NC$ (50%) |
| $B$ | $NC$ (100%) |
| $C$ | $NB$ (100%) |
My failure to realize the Jailer’s answer is also a random variable and to model its behavior properly is the reason why I came up with the wrong answer.
Why Data Analysts are important and a step-by-step guide to do probabilistic reasoning
This realization about the nature of probabilistic models helps me better appreciate the role of Data Analysts in data science teams. Usually, data analysts are the people who are responsible to collect the data and understand how it was generated from business/operation processes. Meanwhile, data scientists uses that data to build predictive models. We often value data scientists a lot for their ability to build machine learning models that learn patterns from the data.
Through this example, I realized that the knowledge of data-generating processes that analysts prossess is also of vital importance to building good models. Without it, a model might perform very well on paper (accuracy, precision, recall, mse, etc.) but does terrible in the real world.
In addition, I also list out a process to reliably update belief without getting into the mistakes that I made:
- Step 1: What are the Observations (O)?
- Step 2: What are the possible Ground truths (G)?
- Step 3: How could those observations be generated from the ground truth?
- Step 4: From step 3, create a probabilistic mapping from G to O.
- Step 5: Using Bayesian analysis to find the answer.
Referrences
[1] The 3 prisoner problem (https://www2.isye.gatech.edu/~sman/courses/6739/)

